Most people like


 5.3K
5.3K
 18.88%
18.88%
 2
2


 90.8K
90.8K
 50.53%
50.53%
 4
4


 < 5K
< 5K
 1
1
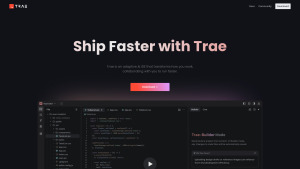

 1M
1M
 44.54%
44.54%
 1
1
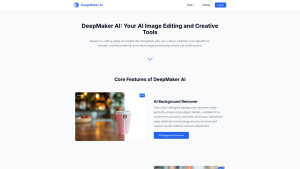

 < 5K
< 5K
 4
4
- App rating
- 4.9
- AI Tools
- 100k+
- Trusted Users
- 5000+
 WHY YOU SHOULD CHOOSE TOOLIFY
WHY YOU SHOULD CHOOSE TOOLIFY
TOOLIFY is the best ai tool source.
- 英特爾酷睿i5 4430哈斯威爾處理器評測
- 100°C成為新常態!Intel Core i9-13900K對比i9-12900K以及Ryzen 9 7950X
- Intel 迫切需要另一款 2500K 處理器
- AMD Ryzen 6000、7000流言爆料!GTC回顧
- 2024年頂尖遊戲處理器推薦!
- Dell Precision 5530|SSD 1TB|RAM 32GB|I7 8850H|Quadro P1000|4K 15.6吋|像全新98%
- 超頻 AMD 1055T Phenom II X6
- 4萬台幣最佳筆記型電腦評估與比較
- AMD Ryzen 7800 X3D比Intel 13900K快25%!
- AMD 1055T 七年後仍能上遊戲嗎?



































